
Am Fam Physician. 2021;103(1):7-8
Original Article: Beware of False-Positive Results with SARS-CoV-2 Antibody Tests [Letter to the Editor]
Issue Date: July 1, 2020
Available at: https://www.aafp.org/afp/2020/0701/p5a.html
To the Editor: We read with interest the warning issued by Drs. Ebell and Barry regarding false-positive rates in antibody testing in their Letter to the Editor. We agree that testing in low-prevalence populations will result in a large number of false-positive test results. Because multiple definitions of the false-positive rate exist, it is important to state which definition is being used.1
We are most familiar with the false-positive rate being defined as the complement of the specificity as in the evidence-based medicine glossary provided by American Family Physician.2–4 Using this definition, Table 1 from their letter, which “summarizes the false-positive rates at various population prevalence [levels],” does not make sense because specificity does not change with prevalence. The middle column of Table 1 lists a specificity of 96%; consequently, the false-positive rate should be 4% in all of the cells. The right column of Table 1 lists a specificity of 99%; consequently, the false-positive rate should be 1% in all of the cells. We agree that specificity may change based on other patient characteristics, and that patient characteristics may affect the estimate of the prevalence used in the calculations.
The definition of the false-positive rate used in Table 1 and in the text of their letter is the proportion of positive tests that are falsely positive, which in effect is the complement of the positive predictive value. Because the positive predictive value increases with the prevalence of the disease in the population, then, as shown in Table 1, the complement of the positive predictive value would decrease with the prevalence. We agree that this definition of a false-positive rate leads the reader to the relevant clinical question5; if the test result is positive, what is the probability that the disease is present?
Similar to the HIV epidemic, the severe acute respiratory syndrome coronavirus 2 that has caused the current pandemic has brought the diagnostic process to the forefront of academic and lay discussions. We believe it is essential to recognize that the differing definitions of false-positive rate can have profound implications for public health and clinical decision-making.1
In Reply: Thank you for your thoughtful commentary on our research letter. We agree that the common use of the term false-positive rate is to describe the converse of specificity (i.e., one minus specificity). In the accompanying table, we list commonly used parameters for test accuracy.
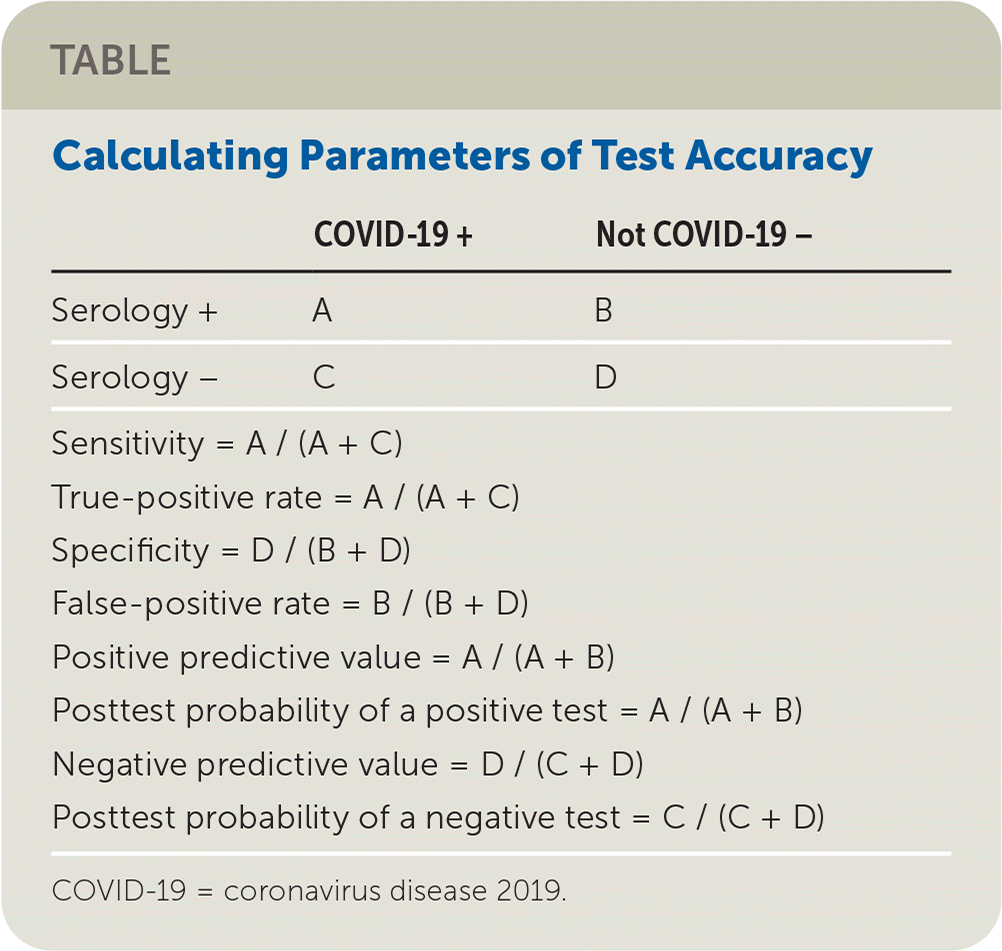
| COVID-19 + | Not COVID-19 − | |
|---|---|---|
| Serology + | A | B |
| Serology − | C | D |
| Sensitivity = A / (A + C) | ||
| True-positive rate = A / (A + C) | ||
| Specificity = D / (B + D) | ||
| False-positive rate = B / (B + D) | ||
| Positive predictive value = A / (A + B) | ||
| Posttest probability of a positive test = A / (A + B) | ||
| Negative predictive value = D / (C + D) | ||
| Posttest probability of a negative test = C / (C + D) | ||
The false-positive rate is commonly calculated as B / (B + D), which Dr. Stovitz and colleagues point out is the converse of specificity. For example, in a receiver operating characteristic curve, we plot the true-positive rate vs. false-positive rate. However, we were trying to communicate the likelihood of a false-positive test among all patients with a positive test. This is also a false-positive rate (actually, a ratio, but let's not quibble), just not the one commonly used in textbooks. There is no commonly used term for our false-positive rate, which is B / (A + B), so we took the liberty of also calling it a “false-positive rate.”
